数值入门篇:掉落方式
电脑随机和物理随机
在真实的物理世界中,将一枚硬币扔上天空,谁也不能确定落下的是正面还是反面,这就是随机事件,其结果是不可预测的。
但在计算机世界里我们能通过算法来解决这个问题。严格来说计算机中的随机函数是按照一定算法模拟产生的,计算机随机函数所产生的“随机数”是一种伪随机数。
数值策划在工作过程中要时刻保持对数值的敏感。一旦随机值出现很大偏差,最好和程序员一起检查一下目前的随机算法。对具体算法感兴趣的读者可以自己上网查找资料,我们在这里不对这个方向进行展开说明。
游戏内掉落随机的几种做法
我们在游戏中会采用不同的随机方式。而玩家感觉起来像随机的事件其实也不完全是按随机事件来设计的。下面来谈谈这些做法。
计数随机
在早期游戏中,有些道具的掉落是和怪物被击杀的次数相关的,通常在成千上万次的击杀后掉落某些物品。如果玩家并不是特别细心的话是发现不了这种计数式掉落的。
这种做法的好处是只要玩家杀到一定数量的怪物是肯定可以得到回报的,但缺点是这种做法一旦被玩家发现之后,玩家会利用这个设计来达成一些自己的目的。
比如升级装备,玩家会先用一些不好的装备来升级,最后在快要成功的时候,换上自己真正想要升级的装备。而且一旦有几个玩家发现这个做法,那这个技巧就会被快速传播,然后对经济产耗形成巨大冲击。
这种设计在单机游戏中更为多见。而目前市面上的游戏多数都不采用这种设计方法了。
逐个百分比掉落
在早期的MMORPG中,道具的物品种类并没有那么丰富,往往从怪物身上掉落的物品不会超过5种(此处是种类不是数量)。
这时候比较流行的掉落方式是逐个百分比掉落。假设我们有A、B、C、D这4个道具,那么我们会先计算A是否掉落,然后计算A掉落的数量,再计算B是否掉落以及掉落的数量,直到所有道具循环完毕。看下实例,先设置概率最大掉落、最小掉落的数量,如图1-2-1所示。
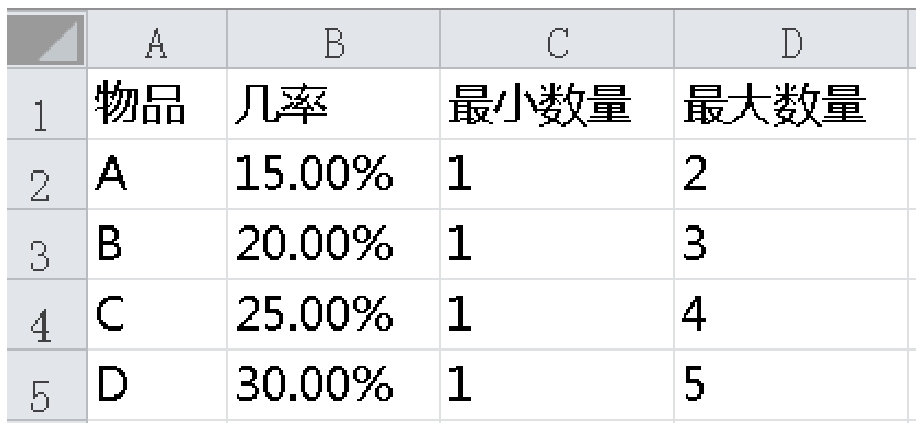
A、B、C、D的掉落概率分别为15%、20%、25%、30%。当确定A掉落后,掉落数量的概率是均等的,掉1个和2个的概率分别为50%。
接下来我们用公式模拟随机数。还记得之前章节所介绍的函数RANDBETWEEN吗?在这里使用这个函数来模拟随机数。然后和概率进行对比,如果小于等于概率则生成掉落,大于则代表没有掉落。
要注意一点,这里要用到4个随机数而不是1个。为什么要用4个而不是1个?我们希望不同物品的随机事件是独立的而不是互相影响的。如果只用一个随机数会发生什么结果?一旦掉落了物品A,那么势必B、C、D全部都会掉落(掉落A证明随机数是小于15%的)。这样的体验是非常诡异的,一个良好的体验肯定是让玩家尽量在每次掉落中都能获取物品。为了达到这样的设计目的明显不能只用一个随机数。
采用4个随机数得到如图1-2-2所示的一组随机数。
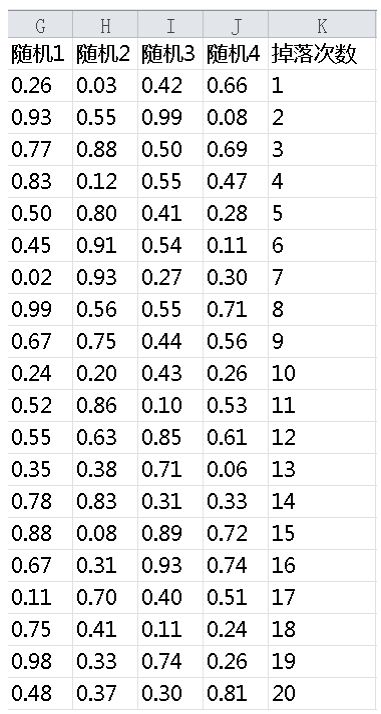
一共模拟1000次掉落的结果,随机值公式如下:
f(x)=RANDBETWEEN(1,100)/100
随机1这一列将会作为判断物品A是否掉落的随机数,以此类推,随机4判断物品D。然后用随机值和概率进行对比,判断公式如下。
L2中公式:=IF($B$2<=$G2,0,RANDBETWEEN($C$2,$D$2))M2中公式:=IF($B$3<=$H2,0,RANDBETWEEN($C$3,$D$3))N2中公式:=IF($B$4<=$I2,0,RANDBETWEEN($C$4,$D$4))O2中公式:=IF($B$5<=$J2,0,RANDBETWEEN($C$5,$D$5))
然后选中这4个单元格下拉,拖至1000个数据。此时得到如图1-2-3所示的一组数据。
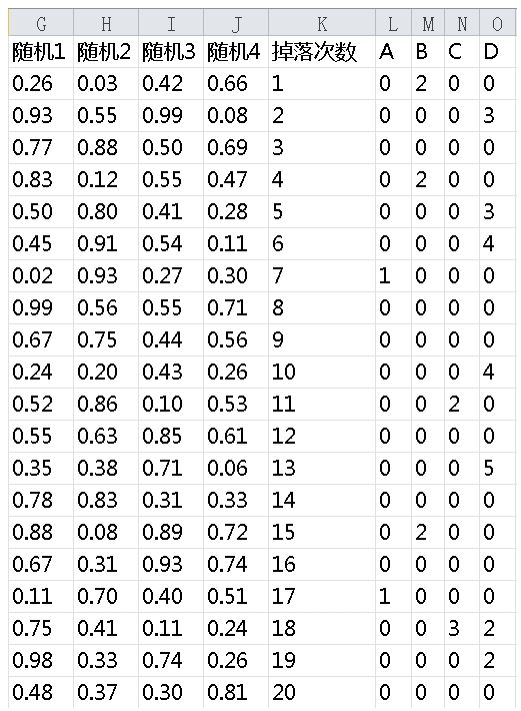
我们来看掉落次数1这一行,数据代表了掉落2个物品B。再看掉落次数18这一行,代表了掉落3个物品C和2个物品D。
下面来统计一下1000个掉落中共掉落了多少物品。首先按公式算出预期值。E2公式如下:
=1000*B2*AVERAGEA(C2:D2)
先算出平均掉落次数,然后乘以平均每次掉落数量得出千次掉落的理论值,如图1-2-4所示。
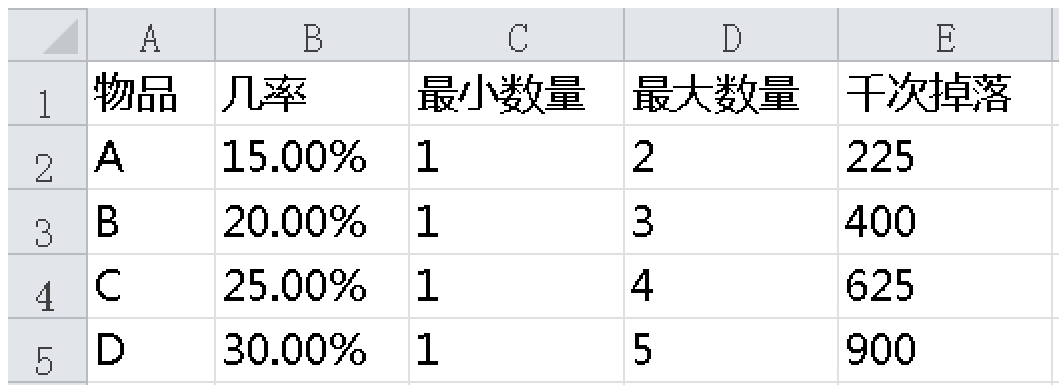
然后再来统计掉落中的物品数量,用理论值除以实际值,如图1-2-5所示。
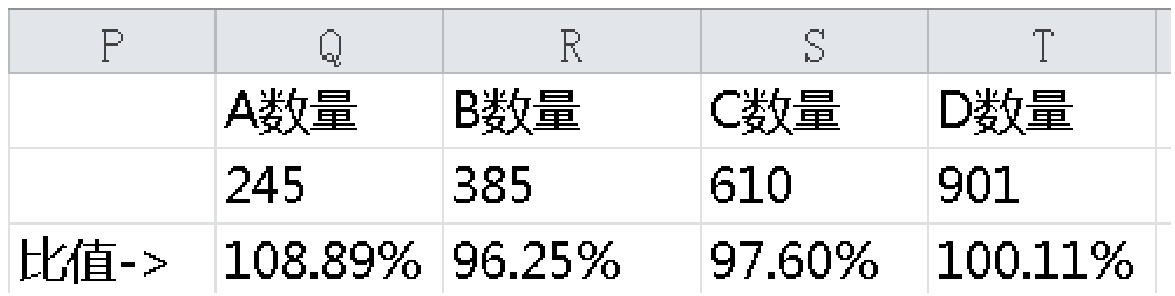
从图1-2-5中可以看到误差并不是十分大,这也证明我们的设计是合理的。由此可以看出这个设计的好处,它非常易于理解并且对于单个物品的总体产出是很稳定的。但它有一个问题,无法控制掉落组合的精确数量,比如我们想要掉1个A加1个B的概率是5%,则是无法做到的。这种设计更加适合关卡掉落,而不适合用在礼包掉落。
权重掉落组式掉落
由逐个百分比掉落引出的问题是无法配置精确的组合,于是我们找到了一种可以解决这个问题的掉落方式:权重掉落组式掉落。
之前逐步掉落方式思路是这样的,循环判断每个道具的概率,然后把它们放进一个掉落包中,接着掉落这个掉落包。逐步掉落式的流程图如图4-36所示。
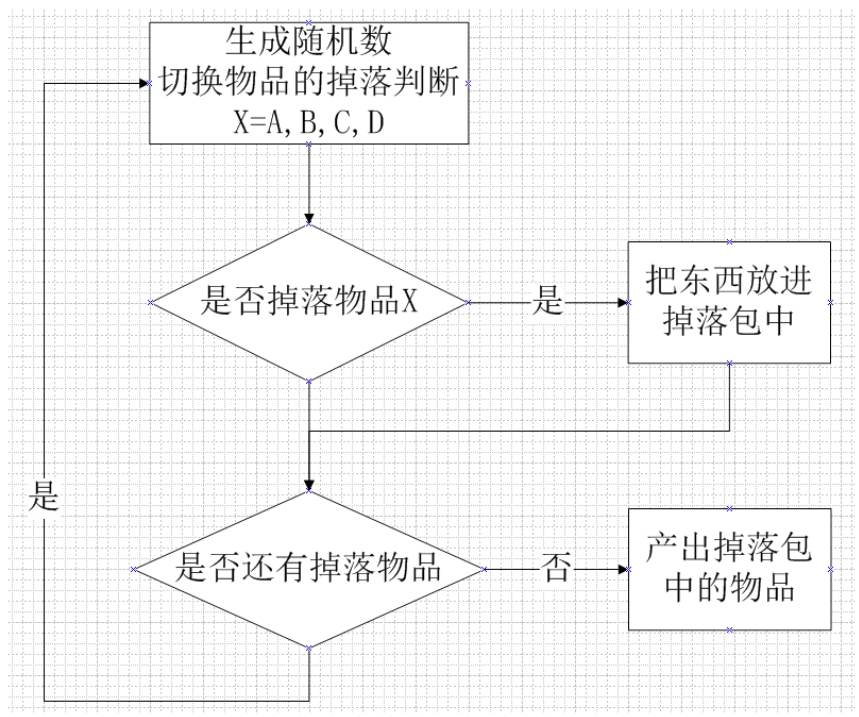
下面来看看权重掉落组式掉落的思路是什么样的。从图1-3-2可以看出和逐步掉落式的流程是非常接近的,但是它多了一步,它拥有母集和子集的概念。
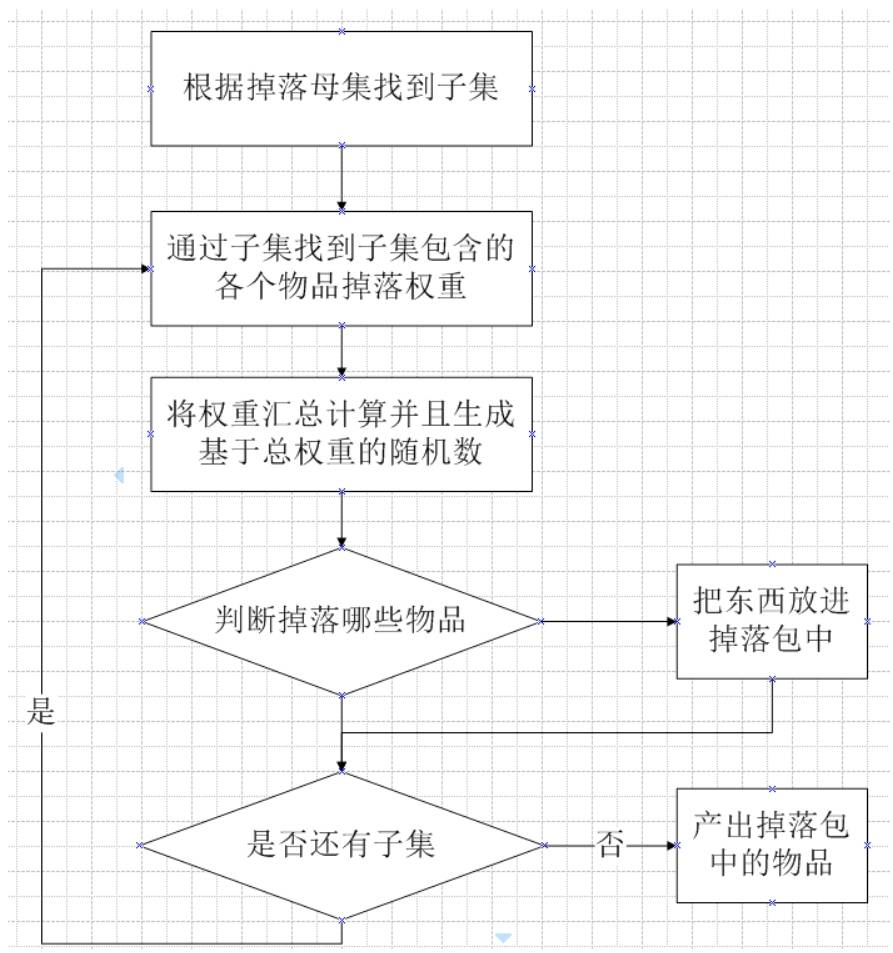
具体实现环节来解析一下。之前看到的掉落设计方式其实都是单表,而权重掉落组式掉落拥有两张表。先来看一下母集表,如图1-3-3所示。
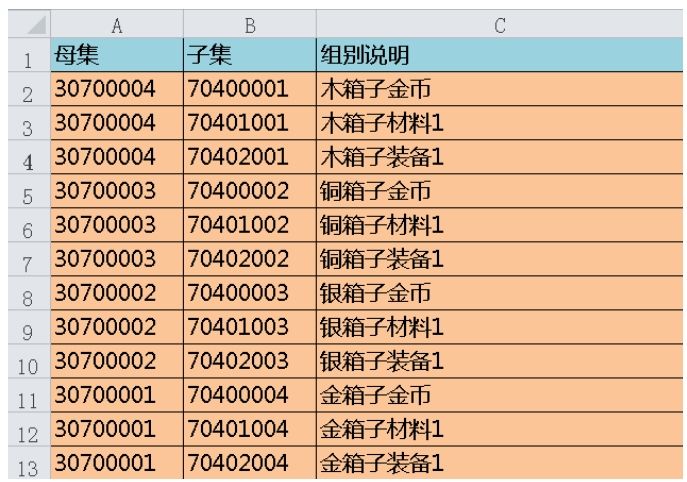
母集中掉落编号30700004产生了3个子集,它们分别代表一个木箱子中可能会掉落的金币、材料和装备。然后根据3个子集的编号在子集表中寻找道具以及对应的权重。子集表如图4-39所示。
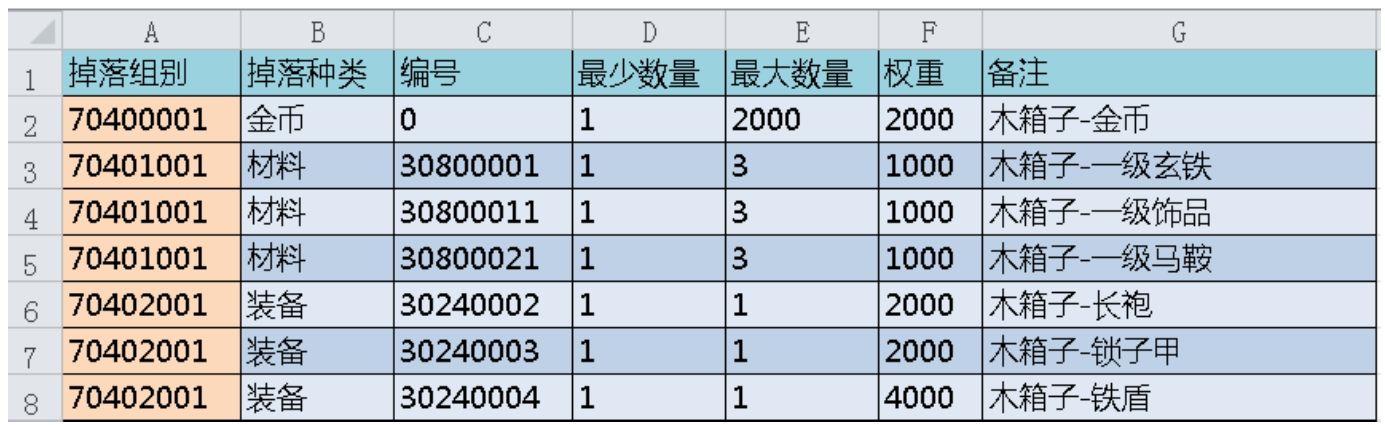
看看第一个子集,它掉落的是金币,首先看权重,这里只有一条数据,那掉落的只能是它,然后再从最小数量和最大数量之间确定随机掉落数量。此处相当于开木箱会100%获得金币,如果想要玩家只有50%概率获得金币,可以再加入一条权重2000的空掉落集。根据流程会先判断子集中掉落哪一种道具,最后再根据道具掉落的最大和最小数量算出随机掉落数量。
按权重掉落和前面的“圆桌理论”的实现方式有些类似。下面再来看第二个子集,它拥有3个掉落选择,先把掉落玄铁、饰品、马鞍的权重值加在一起得到权重总值3000,然后随机获得1~3000中的一个数值。当这个数值小于等于1000的时候掉落玄铁,大于等于1001小于2000的时候掉落饰品,大于等于2001小于3000的时候掉落马鞍。最后根据道具掉落的最大和最小数量算出随机掉落数量。
这里要注意一个问题,在配置道具的时候一定要配置好它们对应的道具类型。类型将决定程序去哪张表寻找道具,如果配置错误会导致找不到这个掉落道具。而更为严重的问题是,有些程序会直接跳过这条Bug不做任何报错,这就会导致预期的掉落物品实际上根本没有掉落。这会对经济系统的投放产生很大影响,所以请大家一定要杜绝这种问题的发生。
第3个子集的计算流程也是一样的,我们从权重中可以看出铁盾的掉落概率为50%,长袍和锁子甲的掉落概率各为25%。
最后,我们把3个子集的物品放在一起形成最终的掉落。
这种设计的优点在于你可以灵活地组合各种子集,从而形成一个非常丰富的掉落组合,并且不管是任何系统关联的掉落都可以只用一个母集的编号来对应。这对程序维护成本和程序效率是大有帮助的。缺点是母集和子集之间关联性强,容易出现数据问题,对数值本身要求较高。
进阶掉落
权重掉落组式掉落是目前较为主流的做法,但随着游戏的不断发展,我们遇到了新的问题。比如某玩家想要获得某关键武器A,可是他的运气十分差,在多次击杀相关BOSS之后就是不掉落武器A。玩家十分恼怒,并最终打电话向客服投诉(非常真实的案例)。
客服反馈了这个问题,但权重掉落组式掉落中数值策划是无法控制某物品必然掉落的,此时我们就结合计数掉落设计出了进阶掉落方式来解决这个问题。
进阶掉落其实是在权重掉落组式掉落的基础上做了进化的版本,核心思想还是一样的,它多了一步前置判断,在每次母集掉落之前会判断一次母集是否满足一定条件并产生进阶掉落。进阶掉落流程图如图1-4-1所示。
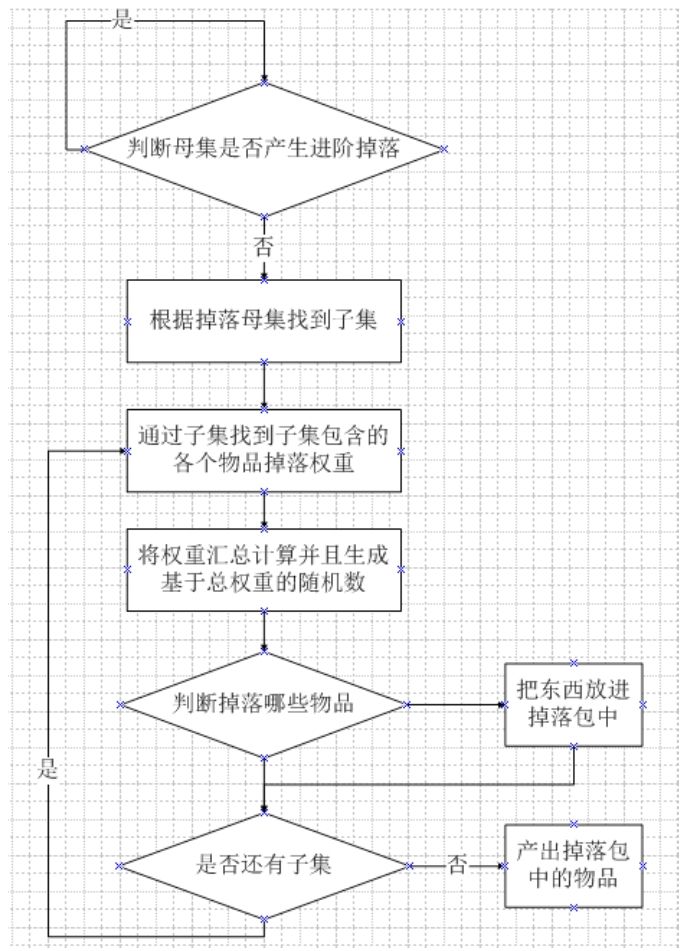
如何判断是否产生进阶掉落?我们在母集表中先添加3列数据:进阶组别、最小进阶次数、最大进阶次数,如图1-4-2所示。
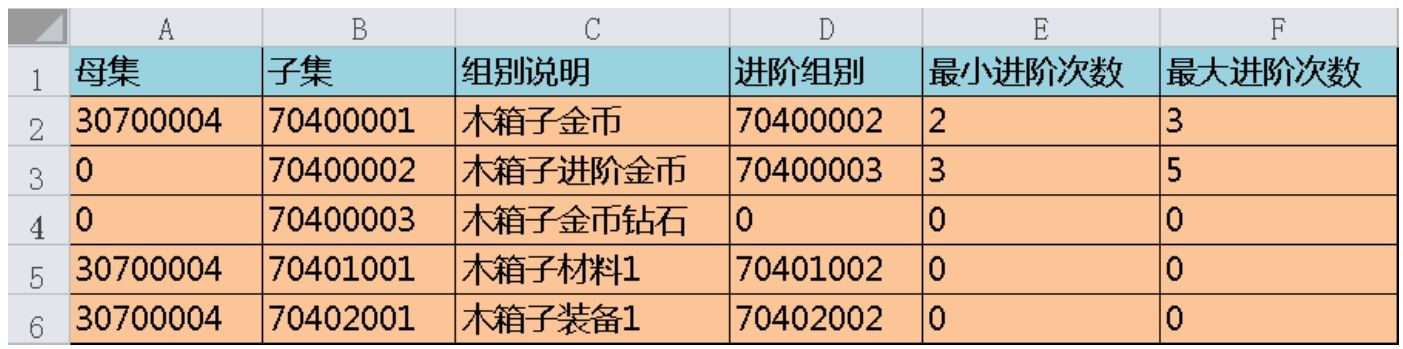
先看第1行数据,母集有一个70400001的子集,这个子集里装的是金币,它对应的进阶母集是70400002,70400001进阶到70400002最少需要2次,最多需要3次。
有些人会质疑如何保证在这个进阶次数区间内就一定进阶。下面来解释一下这个流程。假设最小进阶次数为a而最大进阶次数为b。然后统计出掉落次数x,再获取一个a~b之间的随机数y,之后判断x是否大于等于y,是的话产生进阶掉落,不是的话还是掉落原来的母集,流程图如图1-4-3所示
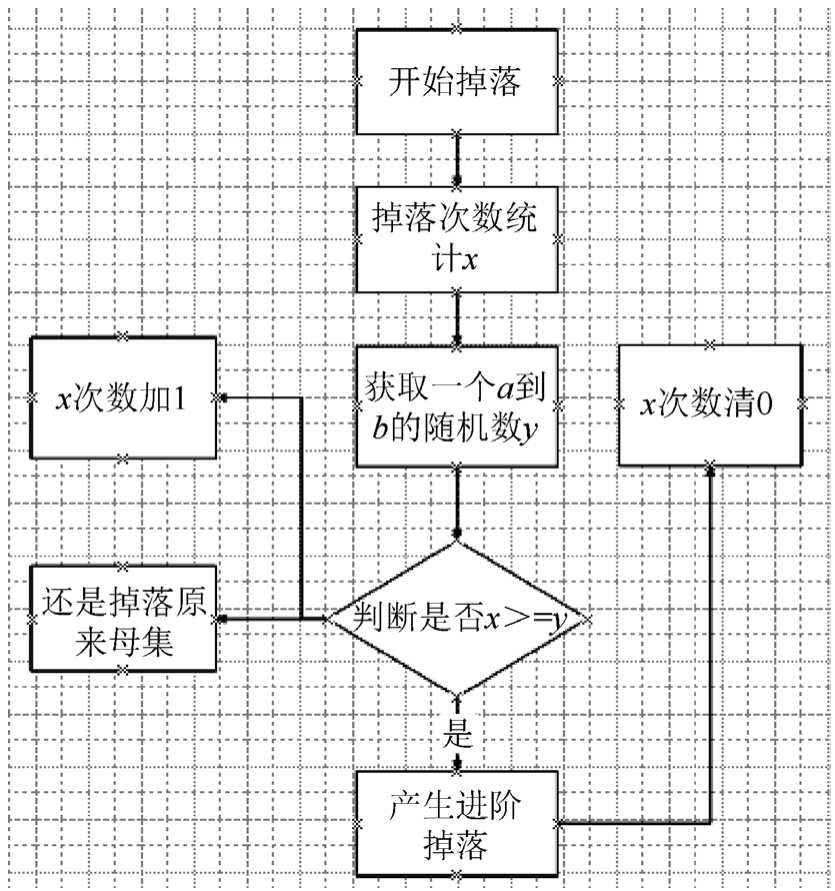
下面套用这个流程再来看之前的数据。
条件如下:
a=2
b=3
第一次掉落开始,x=1,开始第一次掉落。y随机取2,判定失败,还是产生之前的掉落。
第二次掉落开始,x=2。y随机取3,运气真是太差了,如果随机取2判定就成功了,失败之后还是产生之前的掉落。
第三次掉落开始,x=3。y随机取2,判断成功,产生进阶掉落,另外x的次数被重置为0。
这里大家可以看到在第二次掉落开始的时候,如果随机取2的话,这时就会发生进阶掉落。第三次掉落的结果则是必然成功的。这就保证掉落次数达到最大进阶次数时必定发生进阶。
进阶掉落其实是可以叠加多次的。还是之前的数据,70400001进阶70400002所用的次数是2或3次,再来看70400002进阶到70400003需要3~5次,可以算出70400001进阶到70400003需要6~15次。这也就意味着,我们每打开6~15个木箱子,就会得到1次掉落钻石的机会,钻石的数量为20。这样就可以计算出从木箱子获得钻石的期望为每打开10.5个木箱子可得到20个钻石。1个木箱子约含有2钻石的价值,如此玩家获得木箱子的成本必然要大于2钻石。子集表如图1-4-4所示。
进阶掉落是目前很多游戏都在采用的做法。你可以把想要对进阶产生影响的因素通过不同的方式来计算统计,然后使之成为判断进阶条件。比如很多游戏的VIP等级就会对随机产生影响,VIP等级高的人更容易刷出商店中的高级道具。在这里就不对这些元素一一介绍了,其道理和进阶掉落都是一样的。
木桶原理掉落
首先解释一下木桶原理:一个水桶无论有多高,它盛水的高度取决于其中最低的那块木板。这个道理也往往被人称为短板效应。而在游戏中玩家会遇到非常多的道具,可往往自己心里想要得到的道具总也不掉落。木桶原理掉落就是用来解决这个问题的,木桶原理掉落让你最短缺的道具有更高的掉落概率。
在这里说明一下,木桶原理掉落是笔者自己根据《皇室战争》这款游戏反推出来的,可能会和真实游戏的设计方案有一定的误差,请大家谅解。
首先介绍一下流程。在确定它们的权重之前,要先计算预期量和现有量是多少,再计算空缺量是多少。之后根据空缺量计算出空缺率是多少,空缺率非常大的道具会获得额外的系数加成。最后由空缺量乘以系数加成算出掉落权重。木桶原理掉落流程图如图4-44所示。
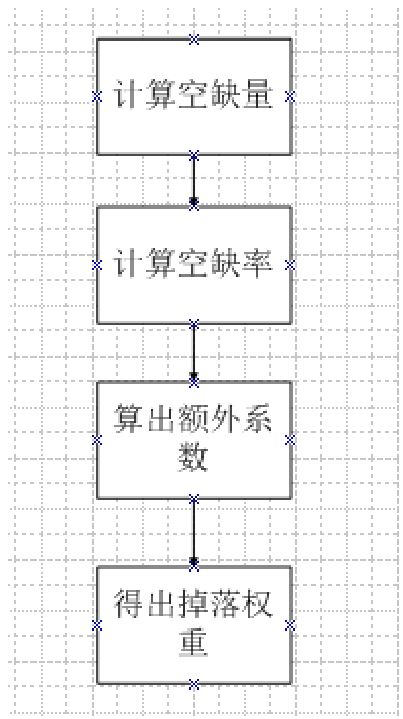
再来看一下如图1-5-2所示的表格。

预期量是我们根据游戏的进度来决定的期望让玩家得到多少该类型道具。现有量是统计目前玩家得到多少道具的数值。然后算出空缺量公式:
空缺量=预期量-现有量
空缺量最小值等于10,我们不希望道具在达到我们的预期量之后一点权重都没有。然后根据空缺量算出空缺率:
空缺率=空缺量/预期量
再根据空缺率算出系数加成,笔者在这里思考的是如果空缺量大于等于90%,则证明该道具是极度空缺的,系数加成为4,而空缺量大于等于70%小于90%为较空缺,系数加成为2,另外其他比例的系数加成为1。再用之前算出来的空缺量乘以系数加成得出最终的权重。
可以看到道具1由于空缺大所以它的掉落概率是最高的,然后是道具4,但是其他道具也是有机会掉落的。最终掉率符合我们的设计预期。
战斗系统中随机的运用
前面给大家介绍了一些随机方案,下面对系统中的随机运用做一个讲解。
以传统MMORPG来说,战斗系统会在如下的情况下运用到随机。
1.决定闪避用到的随机值。
2.决定暴击用到的随机值。
3.决定攻击从上限到下限的随机值。
一般以上情况用的都是系统自带的随机数,但有些游戏会将第3种随机值做一定处理。因为某些游戏的攻击范围较大,设计者不希望让玩家的攻击输出变得特别不稳定。
具体实现方式也是比较简单的,我们将攻击的结果进行多次随机取值并且取其平均值,但次数也不宜过多,一般取3~5次。这样所得的结果比随机一次要平滑很多。下面来看一下两种做法的曲线对比图,如图2-1所示。
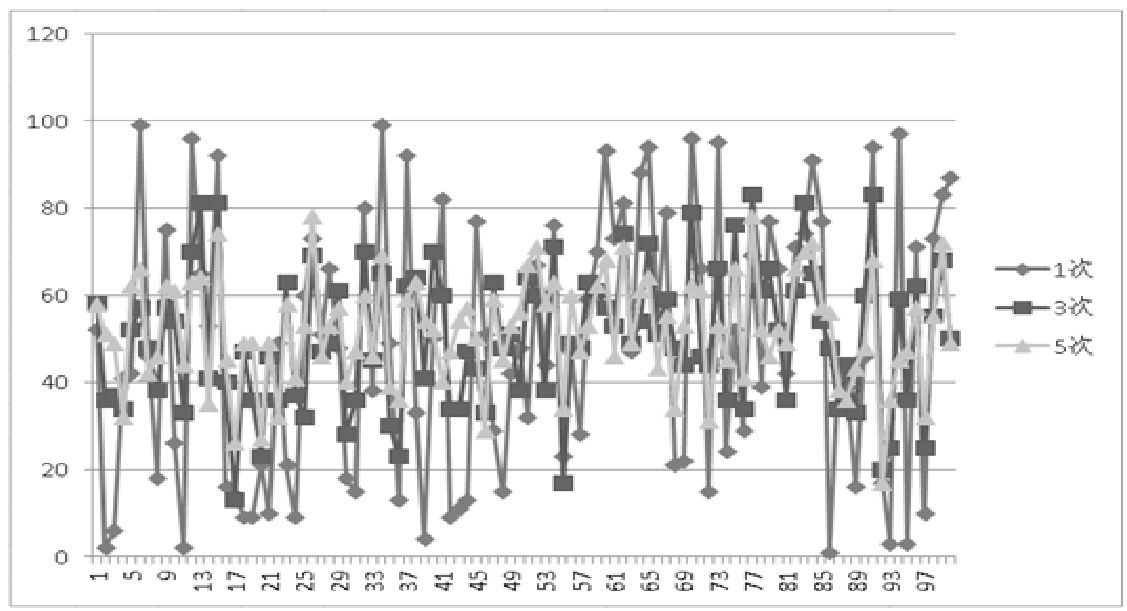
我们取1~100的100个随机数,然后计算1次平均值、3次平均值和5次平均值。大家可以清晰地从图4-46中看出,1次平均值波动较大,5次平均值波动较小。
5次平均值只有一次攻击超过了80,它的大部分攻击在20~80之间,它的输出会更加稳定。
再来看一下对比,统计上述3种情况进行4次攻击的和,统计次数为1000次。从理论上来讲,我们进行1~100攻击的平均攻击为50.5,4次攻击和的期望值为202。然后统计真实结果超过对比值的情况出现多少次,实例如图2-2所示。
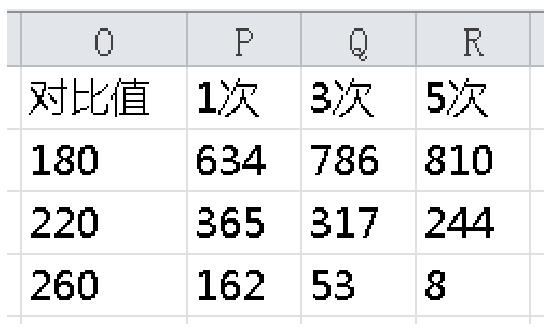
我们发现一个非常明显的趋势,1次平均值的结果超过260的次数是最多的,但超过180的次数是最少的。5次平均值的结果超过260的次数非常少,超过180的次数是最多的。
换个角度来思考,把这个对比看成是一个杀怪过程。杀一个260生命值的怪物,用1次平均值的方法每1000次有162次可以用4次击杀怪物。但用5次平均值的方法,每1000次有8次可以用4次击杀怪物。同样的方式进行对比,杀一个180生命值的怪物。用1次平均值的方法每1000次有634次可以用4次击杀怪物,用5次平均值的方法有810次可以用4次击杀怪物。
用1次平均值的方法,我们有更大机会击杀生命值高的怪物,但击杀生命值低的怪物则要用相对更多的次数。5次平均值则相反。从设计角度讲,我们希望玩家能更稳定地击杀生命值低的怪物,而面对生命值高的怪物时,玩家应该消耗更多的攻击次数来完成击杀。
怪物掉落
之前给大家介绍了几种掉落方式,下面介绍怪物掉落。怪物掉落一般使用的是进阶掉落,但也不是所有子集都进阶。
下面介绍一下我们的设计思路。首先,我们要规划所有的子集类型。举例进行说明。
1.货币子集。 这个子集是控制掉落货币的子集。怪物掉落的货币一般来说是不会有很大波动的,我们可以通过这个掉落来算出每个怪物的产出货币量,最终控制总产出符合我们的预期。这个货币子集可能根据怪物类型不同而不同。比如有些游戏人形生物掉落货币会比动物多,有些游戏动物、植物甚至是不掉落货币的。
2.垃圾材料子集。 早期游戏会有这样的设计,这类材料除了兑换货币之外没有任何作用。为什么会有这类设计,是因为当年的设计者希望通过这种丰富的材料产出来刺激玩家对自己背包空间的追求。这种垃圾材料对于掉落的意义从本质上说和货币子集是一样的,最终都是折算成货币的产出来衡量。
3.材料子集。 这里的材料包含普通材料和宝石等。如果有特殊需要,材料子集也可以分为多个子集。我们会根据材料的稀缺性来决定产出的量级,并且不会让玩家轻易获得珍稀材料。
4.装备子集。 装备子集是玩家非常在意的一个掉落子集。一般情况下,我们会给玩家投放一些基础装备,让他们可以通过日常杀怪获得这些装备。稀有装备有严格的进阶掉落控制,玩家可以在击杀一定量的怪物后获得一件稀有装备。这样可以保证在一定时间内给玩家一个较大的收获,刺激玩家继续杀怪。
还有些游戏会根据自己的需求来分配其他的掉落子集,在这里也就不一一介绍了。设计的原理都是相通的,只要确定设计目的,控制好产出方式和产出量就可以了。